Правильные многогранники
№ 119
(Урок математики в VI классе)
Нилуфар ХАЙРУЛЛИНА,
учитель математики лицея-интерната г. Буинска
Цель урока: дать понятия правильного многогранника, полуправильных и звездчатых многогранников, рассмотреть свойства многогранников, познакомить с историей возникновения и развития теории многогранников.
Задачи урока:
– формирование пространственных представлений, математической культуры, культуры общения;
– развитие практических навыков учащихся по изготовлению правильных, полуправильных, звездчатых многогранников;
– развитие умения наблюдать, умения рассуждать по аналогии, интереса к предмету через использование информационных технологий и осуществление межпредметных связей;
– воспитание общетрудовых умений, графической культуры, умения работать в группе;
– формировать понятие правильного многогранника;
– научить определять вид многогранников;
– развивать логическое мышление и творческие способности.
Прогнозируемые результаты:
– знать определение правильных выпуклых многогранников;
– уметь доказать, что существует всего пять видов таких тел;
– уметь охарактеризовать каждый вид правильных многогранников;
– знать теорему Эйлера (без доказательства);
– уметь решать задачи на нахождение элементов правильных многогранников.
Оборудование: медиапроектор, презентация учителя, которая может применяться и на последующих уроках для проверки знаний; правильные многоугольники из бумаги, развертки правильных многогранников, пластиковые палочки, пластилин, бумажные полоски цветной бумаги для составления тетраэдра и куба.
Примечание. Уроку предшествует очень большая подготовительная работа. Некоторые учащиеся получают задание подготовить рефераты и сообщения по конкретным темам истории математики. При этом учитываются индивидуальные особенности детей, их предметные наклонности. Учитель проверяет рефераты и оценивает работу учащихся. Таким образом, оценки учащиеся могут получить не только за работу на уроке, но и за подготовку реферата.
| Этапы урока | Деятельность учителя | Деятельность учащихся | Формируемые УУД | ||||||||||||||||||||
| I. Этап мотивации (самоопределения) к учебной деятельности. | Приветствие учащихся, проверка готовности к уроку.
Эпиграф к уроку: «Одна из заповедей Пифагора: «Не делай никогда того, чего не знаешь, но научись всему, что следует знать». Слайд 1 |
Приветствие учителя, настрой на работу | Л: самоопределение;
Р: целеполагание; К: планирование учебного сотрудничества |
||||||||||||||||||||
| II. Этап актуализации и пробного учебного действия. | – Давайте попытаемся выполнить следующее задание:
– Попробуйте из минимального количества спичек собрать четыре треугольника.
– Итак, посмотрим, что у вас получилось?
– Что вы можете сказать о данной фигуре?
– Верно. Как называется данная фигура?
– Из чего состоит поверхность данной пирамиды? (Три грани опираются на четвертую.) – Как называются эти треугольники? – С какими пирамидами вы знакомы из истории? – Из минимального количества спичек собрать шесть квадратов. – Из минимального числа спичек собрать 8 треугольников.
– Какие фигуры называются правильными? – Перед вами развёртки различных тел, склейте их Попробуйте подобрать общее название для них- это будет наша тема урока. Слайд 3 |
Учащиеся выполняют задание с помощью палочек и пластилина (учитель контролирует деятельность учащихся).
Учащиеся демонстрируют фигуру.
— состоит из 4 одинаковых треугольников (правильных); объемная. — ПИРАМИДА
– Из правильных треугольников – Грани пирамиды – Египетские пирамиды (четырехугольные пирамиды)
Работа в парах – Правильные многогранники |
К: планирование учебного сотрудничества с учителем и сверстниками
Познавательные: самостоятельное выделение и формулирование познавательной цели.
Логические: формулирование проблемы |
||||||||||||||||||||
| III. Этап целеполагания (выявление места и причины затруднения) | Однажды, один мальчик, увлекшись изготовлением моделей многогранников, соединял правильные треугольники и получил фигуры, о которых написал в письме своему отцу:
«…я сделал модели многогранников. Среди них есть тетраэдр, додекаэдр и еще два эдра, для которых не знаю правильного названия». (Слайд 4)
— Что в данном предложении вам уже знакомо? Кто представляет себе что это за фигуры, в названии которых окончание – ЭДР. Вы сейчас возьмете красные стикеры и приклеите их под надписью «Имею представление», а желтые – под надписью «Плохо представляю»
– Какая же будет цель урока?
Узнать, что такое тетраэдр, додекаэдр и познакомиться с другими видами многогранников.
«Правильные многогранники» Слайд 5
– Мальчик, о котором шла речь, стал великим физиком и звали его Джеймс Кларк Максвелл (Выписать на доску.) |
— Слово МНОГОГРАННИКИ — ТЕТРАЭДР, ДОДЕКАЭДР, ЭДР
Клеют стикеры под надписями на доске
Узнать, какие фигуры в названии которых окончание – ЭДР, познакомиться с другими видами многогранников. |
Регулятивные: целеполагание, прогнозирование.
Познавательные: выбор наиболее эффективных способов решения задач в зависимости от конкретных условий.
Личностные: самоопределение. |
||||||||||||||||||||
| IV. Этап построения проекта выхода из затруднения | Работа в парах с развёртками и каркасными моделями
– Заполните оценочные листы
– Треугольная пирамида имеет еще одно название – тетраэдр, т.е. четырехгранник («тетра» – четыре, «эдр» – грань)
– Существуют и другие правильные многогранники:
Октаэдр (восьмигранник, гранью является треугольник) Додекаэдр (двенадцатигранник, гранью является пятиугольник) Икосаэдр (двадцатигранник, гранью является треугольник) Гексаэдр (куб) – Внимание на экран. (Названия фигур – слайды 12 – 15)
|
Названия фигур учитель вывешивает на доску, демонстрирует разноцветные модели этих правильных многогранников. |
Предметные: формирование навыков построения мат.моделей и решения практических задач.
Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками.
Познавательные: моделирование, решение проблемы, построение логических цепей, анализ.
Личностные: планирование учебной деятельности. |
||||||||||||||||||||
| V. Этап реализации построенного проекта | – Что является элементами многогранников?
– Сейчас каждая группа получит по многограннику. – Ваша задача подсчитать число вершин, граней, ребер и заполнить следующую таблицу:
(слайд 18), (слайд 19 – заполненная таблица)
– Совершенно верно, а доказал это удивительное соотношение один из величайших математиков Леонард Эйлер, поэтому формула названа его именем: формула Эйлера. (Выписать на доску.) – Что еще удивительного вы заметили, выполняя эту работу? – Заполните оценочные листы. – Сейчас мы изготовим модель простейшего многогранника без склеивания элементов данной фигуры.
– Перед вами лежат две полоски разного цвета. Согните и разогните каждую из полосок по пунктирным линиям, чтобы образовались сгибы. Наложите цветную полоску на белую. Сложите из белой тетраэдр так, чтобы цветной треугольник оказался внутри него, а затем оберните цветной полоской две грани тетраэдра и оставшийся треугольник вставьте в щель между двумя белыми треугольниками.
|
– Вершины, ребра и грани.
Учащиеся после подсчетов заполняют таблицу. Выполнив подсчет, учащиеся делают вывод: для всех многогранников один и тот же результат — 2
— У каждого многогранника все грани – правильные многоугольники, в каждой вершине одного многоугольника сходится одно и тоже число ребер.
— учащиеся выполняют задание вместе с учителем. Учитель помогает справиться с затруднительными моментами.
Учащиеся должны получить объемный многогранник. |
Предметные: формирование навыков построения математических моделей и решения практических задач.
Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками.
Познавательные: моделирование, решение проблемы, построение логических цепей, анализ.
|
||||||||||||||||||||
| VI. Этап рефлексии учебной деятельности | – Домашнее задание выберите то, которое вам интересно и по силам:
1. Октаэдр выполнен из проволоки. Найти длину проволоки из которой выполнен октаэдр? 2. Высчитать площадь поверхности куба (додэкаэдра). 3. Высчитать площадь поверхности тетраэдра, — Какую цель мы ставили сегодня на уроке?
– Я вам сейчас предлагаю посмотреть на свои стикеры и если у вас поменялось мнение, их переклеить. Если не поменялось оставить на месте. Но на своем стикере напишите номер выбранного домашнего задания. А три ученика, переклейте стикеры столбиком, по номерам. Посмотрите, у нас получилась диаграмма, на которой мы видим как мы поняли сегодня урок. Надеюсь, что полученные знания и навыки на этом уроке пригодятся вам в дальнейшем обучении и в жизни.
|
Осуществляют самооценку собственной учебной деятельности, соотносят цель и результаты. | Коммуникативные: умение с достаточной полнотой и точностью выражать свои мысли.
Регулятивные: контроль, оценка, коррекция, выделение и осознание того, что усвоено, что еще подлежит усвоению. Познавательные: умение структурировать знания. Личностные: смыслообразование.
|
Оценочный лист учени___ 6 а класса_________________________________________
1.Правильные многогранники
| Название фигуры | Сколько граней? | Какой фигурой представлена грань? | Сколько вершин? | Сколько рёбер? | |
| 1 |
|
||||
| 2 |
|
||||
| 3 |
|
||||
| 4 | 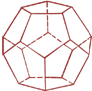 |
||||
| 5 | 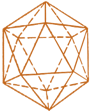 |
Формула Эйлера
|
Правильный многогранник |
Число |
||
| граней и вершин
(Г + В) |
рёбер
(Р) |
(Г+В) — Р | |
| Тетраэдр | |||
| Гексаэдр | |||
| Октаэдр | |||
| Додекаэдр | |||
| Икосаэдр | |||