Олимпиадные задания по математике
Алсу РАХМАТУЛЛИНА,
учитель начальных классов и математики Уруссинской гимназии Ютазинского района, заслуженный учитель РТ, почётный работник общего образования РФ
Цель статьи: помочь читателю обогатить свой опыт в решении олимпиадных задач.
Дальнейшее развитие российской науки существенно зависит от притока талантливых исследователей, поэтому так важно уже в школе поддерживать интерес детей к знаниям, выявляя особо одарённых учащихся. Ведь именно в этот период проявляются и активно развиваются склонности, способности, таланты.
Одной из наиболее эффективных форм внеурочной работы, способствующих повышению интереса школьников к знаниям, развитию их способностей, являются олимпиады. Они стимулируют учебную деятельность. Искусственно формируется потребность в знаниях на данном этапе. И если ребёнок захочет выделиться среди других детей, то он начнёт понимать, что для этого ему нужны некоторые знания, например, по математике, уже сейчас. Даже если ребёнок не проявляет каких-то выдающихся способностей к математике, ему все равно будет полезно попробовать свои силы хотя бы на школьной олимпиаде. Соответствующая атмосфера таких мероприятий способна удержать внимание на предмете и повысить его значимость. Оригинальные познавательные и интеллектуальные задания позволяют раскрыть способности школьников, повысить их интерес к различным наукам, развить творческую инициативу. Ниже приведены олимпиадные задачи и их решения по математике для учащихся 4 – 6 классов.
Комбинаторика
Комбинаторикой или комбинаторным анализом называется область математики, в которой изучаются закономерности между комбинациями, составленными из букв, цифр или любых других объектов и удовлетворяющими некоторым условиям. Идеи комбинаторного характера имеют самое широкое распространение в математике, в таких ее разделах, как теория вероятностей, теория чисел и т.п.
Пример 1. Какие двузначные коды можно составить из букв А, Б, В, Г, Д, Е, Ж, З, И, К, если на первом месте может стоять гласная, а на втором – согласная?
Решение. Выпишем все комбинации, которые можно составить из этих букв указанным способом. Чтобы ничего не пропустить, упорядочим перебор с помощью таблицы.
| Б | В | Г | Д | Ж | З | К | |
| А | АБ | АВ | АГ | АД | АЖ | АЗ | АК |
| Е | ЕБ | ЕВ | ЕГ | ЕД | ЕЖ | ЕЗ | ЕК |
| И | ИБ | ИВ | ИГ | ИД | ИЖ | ИЗ | ИК |
Из таблицы видно, что таких кодов 21.
Ответ. 21 код.
Пример 2. Сколько существует различных паролей, состоящих из четырех различных букв, если в пароле могут быть использованы только буквы А, Б, В, Г?
Решение. Рассмотрим сначала случай, когда на первом месте нашего пароля стоит буква А. В данной задаче пароль четырёхзначный, и для того чтобы выписать все возможные варианты с этой буквой, таблица уже не подойдет. Поэтому составим для этого следующую схему:
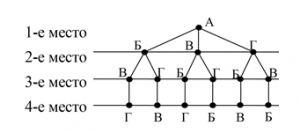
Из схемы ясно видно, что в этом случае на втором месте могут стоять только буквы Б, В и Г. Если на втором месте стоит буква Б, то на третьем месте могут стоять только буквы В и Г, а на четвертом, соответственно, буквы Г и В. Аналогично по два варианта получается, если на втором месте стоят буква В и буква Г. Таким образом, общее число возможных вариантов в случае, когда на первом месте стоит буква А, равно шести: АБВГ, АВБГ, АГБВ, АБГВ, АВГБ, АГВБ.
Поскольку согласно условию задачи никаких ограничений на способ расположения букв в пароле не наложено, то аналогичным образом мы получим по шесть различных паролей и в случаях, когда на первом месте будут стоять буквы Б, В или Г.
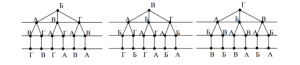
Итак, общее число возможных паролей равно 6⋅4=24. Все варианты паролей можно выписать из полученных нами схем, двигаясь по каждой из «ветвей» схемы сверху вниз.
Ответ. 24 пароля.
Число перестановок
Пример 3. Девочке мама на завтрак дала конфету, пряник и булочку. Сколько различных порядков «поедания» этих сладостей есть у девочки?
Решение. Очевидно, что всего есть шесть вариантов «поедания» сладостей:
конфета → пряник → булочка;
конфет → булочка → пряник;
пряник → булочка → конфета;
пряник → конфета → булочка;
булочка → конфета → пряник;
булочка → пряник → конфета.
Ответ. 6.
Пример 4. Когда у нас есть всего три предмета, то можно просто перечислить все их перестановки. Но если бы предметов было больше – 5, 10 или даже 100, то выписать все перестановки просто не представляется возможным.
Определение
Перестановкой множества из n элементов называется любой упорядоченный набор всех элементов этого множества. Число перестановок множества из n элементов (обозначается p(n) – это количество различных перестановок этого множества. Найдём общую формулу для числа перестановок из n различных элементов. Если у нас лишь два элемента, то они могут быть расположены всего двумя способами: 12, 21.
Для трёх элементов существует шесть различных способов выписать их в строчку:
123, 132, 213
231, 312,
321.
| 1234
1243 1324 1342 1423 1432
|
2134
2143 2314 2341 2413 2431 |
3124
3142 3214 3241 3412 3421
|
4123
4132 4213 4231 4312 4321
|
Для четырёх элементов аналогично получаем 24 варианта перестановки:
Здесь в каждом столбце перестановки начинаются с одного и того же элемента, после которого идут всевозможные перестановки из трёх оставшихся элементов (которых, как мы убедились ранее, шесть штук). Если мы теперь запишем все перестановки из пяти элементов, то это будет табличка из пяти столбцов по 24 строчки в каждом, т.е. всего 5⋅24=120 перестановок.
Сколько же всего существует перестановок из n различных элементов?
Давайте считать: на первое место можно поставить любой из n элементов, на второе место – лишь (n−1) элемент (любой, кроме того, который уже стоит на первом месте), на третье – (n−2), …, на предпоследнее – один из двух оставшихся, и на последнее место можно поставить только последний элемент. В итоге p(n)=n⋅(n−1)⋅(n−2)⋅…⋅2⋅1
или n! способов переставить n элементов.
Правила суммы и произведения
На вопросы типа «Сколько всего трехзначных чисел, в которых ровно две цифры – девятки» дает ответ комбинаторика.
Правило произведения. Пусть объект A можно выбрать n способами и после каждого такого выбора объект B можно выбрать m способами. Тогда выбор пары (A,B) можно осуществить nm способами.
Правило суммы. Пусть некоторый объект A можно выбрать n различными способами, а другой объект B можно выбрать m способами. Тогда существует n+m способов выбрать либо объект A, либо объект B.
Для ответа на исходный вопрос несложно понять, что следует разделить два случая: когда первая цифра – 9 и когда не 9. Все первые числа будут обязательно отличаться от всех вторых, поэтому количество вариантов можно будет просто сложить.
9х9, 99х – два варианта расстановки девяток, по 9 вариантов цифры в каждом
х99 – всего 8 вариантов, т.к. х – не 9 и не 0.
Ответ: 26 чисел.
Пример 5. Монетку бросают десять раз. Сколько различных последовательностей из орлов и решек может при этом получиться?
Решение. Различных результатов после первого броска два – либо орел, либо решка. После каждого из них результатов второго броска также два. Это означает, что после второго броска может получиться 2⋅2=4 различных исхода. Аналогично, после третьего 4⋅2=23=8 различных результатов. После четвертого – 24, …, после десятого – 210=1024 различных последовательностей из орлов и решек.
Ответ. 1024.
При решении подобных задач получается ответ вида nm, где n и m – некоторые натуральные числа. Такой ответ получается во всех задачах, в которых требуется посчитать количество способов, на каждое из m мест поставить один из n различных объектов. В таких задачах главное не перепутать, что в какую степень следует возводить!
Например, в предыдущей задаче «местом» является номер броска, а «объектом» – сторона монеты – орёл или решка.
Пример 6. В классе 25 человек. Сколькими способами можно выбрать старосту класса и его помощника?
Решение. Старосту класса можно выбрать 25 различными способами. После этого к каждому такому выбору старосты помощника можно подобрать 24 различными вариантами. Итого получаем 25⋅24=600 способов выбрать старосту класса и его помощника.
Ответ. 600.
Рассмотрим еще несколько задач на ту же идею, объединенных общей тематикой, – это так называемые задачи на шахматных досках. Заметим, что для решения этих задач про шахматы, по сути, ничего знать не надо, кроме того, как ходят фигуры.
Пример 7. Сколькими способами можно поставить на шахматную доску чёрную и белую ладьи так, чтобы они не били друг друга?
Решение. Чёрную ладью можно поставить на любую клетку доски – 64 способа. После того как мы поставим эту ладью, для белой останется лишь 49 мест, куда ее можно поставить, так как где бы ни стояла черная ладья, она бьет 15 клеток (считая ту клетку, на которой она стоит). Значит, всего вариантов расстановки двух ладей – 64⋅49=3136.
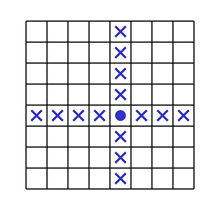
Ответ. 3136.
Пример 8. Сколькими способами можно поставить на шахматную доску черного и белого слона так, чтобы они не били друг друга?
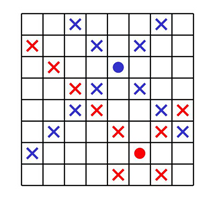
Решение. Заметим, что, в отличие от ладьи, количество полей, которые бьет слон, зависит от того, где он стоит.
Давайте раскрасим всю шахматную доску в четыре цвета, как показано на рисунке, тогда если черный слон стоит на желтой клетке, то он бьет восемь полей (включая то, на котором он стоит), если на красной, то бьет десять полей, если на синей – 12 полей, на зеленой – 14 полей.
Таким образом, если черный слон стоит на желтой клетке (28 различных вариантов), то для белого слона остается 64−8=56 полей, куда его можно поставить. Если чёрный слон на красной клетке (20 вариантов), то у белого слона остается 64−10=54 поля. Если на синей (12 вариантов), то у белого –64−12=52 поля. Если на зелёной (4 варианта), то у белого – 64−14=50 полей.
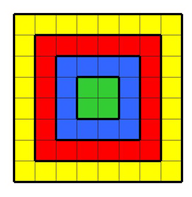
Таким образом, получается всего 28⋅56+20⋅54+12⋅52+4⋅50=3472 способа поставить этих слонов, чтобы они не били друг друга.
Ответ. 3472.
Переливания
(Текстовые задачи)
Задача 9. Однажды Винни-Пух захотел полакомиться медом и пошел к пчелам в гости. По дороге он нарвал цветов, чтобы подарить труженицам пчелкам. Пчелки очень обрадовались, увидев мишку с букетом цветов, и сказали: «У нас есть большая бочка с медом. Мы дадим тебе меда, если ты сможешь с помощью двух сосудов вместимостью 3 л и 5 л налить себе 4 л. Помогите Винни разобраться.
Решение. Наполняем из бочки пятилитровый сосуд медом (1 шаг). Наполняем трехлитровый сосуд, переливая мед из пятилитрового. В итоге в пятилитровом сосуде остается 2л (2 шаг). Выливаем весь мед из трехлитрового сосуда обратно в бочку (3 шаг). Теперь из пятилитрового выливаем 2 л в трехлитровый сосуд (4 шаг). Из бочки наполняем пятилитровый сосуд (5 шаг). И наполняем трехлитровый сосуд доверху из пятилитрового (6 шаг). В итоге в пятилитровом сосуде остается 4 л.
Взвешивания
Задача 10. Из набора гирек с массами 1, 2, …, 101 г потерялась гирька массой 19 г. Можно ли оставшиеся 100 гирек разложить на две кучки по 50 гирек в каждой так, чтобы массы обеих кучек были одинаковы?
Решение. Положим в первую кучку две гирьки массой 101 г и 1 г, а во вторую – 100 г и 2 г; затем в первую две гирьки – 99 г и 3 г, а во вторую – 98 г и 4 г. Так будем действовать, пока не положим во вторую кучку гирьки в 84 г и 18 г. К этому моменту в каждой кучке будет лежать по 18 гирек. Теперь положим в первую кучку две гирьки массой 83 г и 20 г, а во вторую – 82 г и 21 г. Так будем продолжать до тех пор, пока во вторую кучку не придется положить последнюю пару гирек массой 52 г и 51 г.
Ответ. Да.
Задача 11. Лиса Алиса и Кот Базилио – фальшивомонетчики. У Базилио получаются монеты тяжелее настоящих, а у Алисы — легче. У Буратино есть 15 внешне одинаковых монет. Известно, что ровно одна фальшивая. Как двумя взвешиваниями на чашечных весах без гирь Буратино может определить, кто сделал фальшивую монету — Кот Базилио или Лиса Алиса?
Решение. Буратино может разделить свои монеты на три кучки по 5 монет. При первом взвешивании он положит на весы какие-то две кучки монет. Если при этом весы оказались в равновесии, значит, все монеты на весах настоящие, а бракованная монета в оставшейся кучке. Тогда при втором взвешивании на одну чашку весов Буратино положит кучку с бракованной монетой, а на вторую – кучку настоящих монет, и тогда он сразу определит, легче фальшивая монета, чем настоящие, или тяжелее. Если же при первом взвешивании весы оказались не в равновесии, значит, все монеты в оставшейся кучке настоящие. Тогда Буратино уберет с весов легкую кучку, и положит на их место пять настоящих монет. Если при втором взвешивании весы оказались в равновесии, значит, фальшивая монета легче настоящих, а если нет, то тяжелее.
Задача 12. В корзине лежит 13 яблок. Имеются весы, с помощью которых можно узнать суммарный вес любых двух яблок. Как за 8 взвешиваний выяснить суммарный вес всех яблок?
Решение. За пять взвешиваний можно узнать суммарный вес 10 яблок. Осталось найти суммарный вест трех оставшихся яблок. Для этого взвесим первое яблоко со вторым, второе с третьим и третье с первым, затем сложим полученные веса и получим удвоенный вес трех яблок.
Задача 13. Одна из девяти монет фальшивая, она весит легче настоящей. Как определить фальшивую монету за 2 взвешивания?
Решение. Первым взвешиванием мы кладем три монеты на одну чашу весу, три другие на другую чашу весов. Если весы находятся в равновесии, то фальшивая монета среди оставшихся 3 монет, если же одна чаша перевесила, то фальшивая монета находится среди 3 монет на перевесившей чаше. Таким образом, мы нашли три монет, среди которых находится фальшивая. Далее действуем аналогично. На одну чашу весов кладем одну монет, на другую чашу весов кладем вторую. Если чаша весов находится в равновесии, то фальшивой является третья монета. Если же одна из чаш весов перевесила, то фальшивая монета находится на этой чаше.
Разрезания
В задачах на разрезание обычно требуется разрезать данную фигуру на части, обладающие некоторыми свойствами. Оказываются полезными аксиома площади о том, что площадь всей фигуры равна сумме площадей частей, на которые ее разрезали, идея симметрии.
Пример 14. Разрежьте фигуру, изображенную на рисунке, на три равные части так, чтобы линии разреза шли по сторонам клеток.
Решение. Поскольку изображенная на рисунке фигура состоит из 15 клеток, то каждая из равных частей состоит из 5 клеток. Годится, например, такое решение.
Пример 15. Разрежьте фигуру, изображенную на рисунке, на две равные части (линия разреза может идти не только по сторонам клеток, но и по диагоналям).
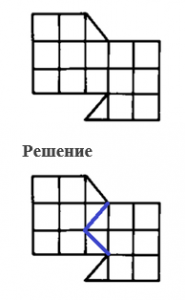
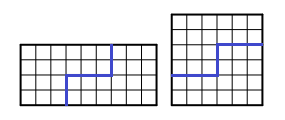
Пример 16. Разрежьте прямоугольник 4×9 по линиям сетки на две части так, чтобы из двух получившихся частей можно было сложить квадрат.
Решение. Поскольку данный прямоугольник состоит из 36 клеток, то сторона квадрата равна 6. Соответствующее разрезание приведено на рисунке.
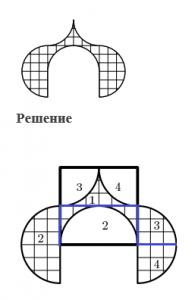
Иногда в задачах на разрезание встречаются более сложные фигуры, граница которых состоит не только из отрезков, но и из дуг.
Пример 17. Разрежьте фигуру, изображенную на рисунке, на части, из которых можно сложить квадрат.
Раскраски
Пример 18. Можно ли из 13 кирпичей 1×1×2 сложить куб 3×3×3 с дыркой 1×1×1 в центре?
Решение. Раскрасим в белый и черный цвет в шахматном порядке маленькие кубики 1×1×1, из которых состоят куб и кирпичи. В 13 кирпичах поровну (по 13) черных и белых кубиков, а в кубе 3×3×3 без центра одних – 12, а других – 14.
Ответ. Нельзя.
Пример 19. Отметьте на доске 8×8 несколько клеток так, чтобы любая (в т.ч. и любая отмеченная) клетка граничила по стороне ровно с одной отмеченной клеткой.
Решение. Будем рассуждать, используя шахматную доску. Заметим, что белые клетки граничат по стороне только с черными, и наоборот. Поэтому сначала отметим несколько белых клеток так, чтобы у каждой черной клетки был ровно один отмеченный сосед:
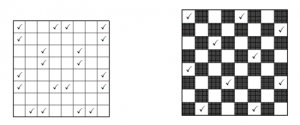
Затем отметим несколько черных клеток так, чтобы и у каждой белой клетки появился ровно один отмеченный сосед (для этого достаточно симметрично отразить отмеченные клетки относительно какой-нибудь средней линии), при этом у черных клеток новых отмеченных соседей не появится.
Ответ. Один из примеров приведен на рисунке:
Пример 20. Доска 8×8 разрезана на доминошки размером 1×2 клетки. Докажите, что количество горизонтальных доминошек четно.
Решение. Назовем клетки первой, третьей, пятой и седьмой вертикалей красными, а клетки второй, четвертой, шестой и восьмой вертикалей синими. Таким образом, в каждой горизонтальной доминошке содержится одна красная и одна синяя клетка, а в каждой вертикальной – либо две красных, либо две синих клетки (назовем в соответствии с этим вертикальные доминошки красными или синими). Поскольку всего красных и синих клеток на доске поровну, количества красных и синих вертикальных доминошек должны быть равны. Следовательно, общее число вертикальных доминошек делится на 2, т.е. четно.
Пример 21. Докажите, что доску размером 10×10 клеток нельзя разрезать на фигурки вида:
Решение. Предположим, что доску10×10 клеток можно разбить на такие фигурки, тогда их будет 100/4=25. Раскрасим доску в шахматном порядке, тогда каждая фигурка содержит либо 1, либо 3 черные клетки, то есть нечетное количество. Но сумма 25 нечетных чисел – это нечетное число. Поэтому 25 фигурок содержат нечетное количество черных клеток. Но всего на доске черных клеток 100/2=50 штук – четное количество. Получили противоречие.
Пример 22. Докажите, что доску размером 10×10 клеток нельзя разрезать на фигурки вида:
Решение. Покрасим вертикали доски через одну в черный цвет. Тогда покрашено 50 клеток. Каждая фигурка, как бы она ни располагалась на доске, занимает нечетное число (либо одну, либо три) белых клеток. Поэтому если бы доску можно было разрезать на 25 таких фигурок, то белых клеток на доске было бы нечетное число (сумма 25 нечетных чисел — число нечетное). Но 50 – четное число. Получили противоречие.
Разбиение на пары
Пример 23. Можно ли нарисовать замкнутую 13-звенную ломаную, каждое звено которой пересекается ровно с одним из остальных звеньев?
Решение. Если бы такое было возможно, то все звенья ломаной разбились бы на пары пересекающихся. Однако тогда число звеньев должно быть четным. Противоречие.
Ответ. Нельзя.
Пример 24. На доске 25×25 расставлены 25 шашек, причем их расположение симметрично относительно диагонали. Докажите, что хотя бы одна из шашек расположена на диагонали.
Решение. Шашки, не стоящие на диагонали, разбиваются на пары симметричных, то есть таких шашек четное число. Так как всего шашек нечетное число, то на диагонали стоит нечетное число шашек, то есть по крайней мере одна.
Пример 25. На доске 25×25 расставлены 25 шашек, причем их расположение симметрично относительно обеих главных диагоналей. Докажите, что одна из шашек стоит в центральной клетке.
Решение. Из решения предыдущего примера следует, что на диагонали стоит нечетное число фишек. Но фишки, стоящие на диагонали, должны располагаться симметрично относительно другой диагонали. Следовательно, одна из шашек стоит в центре доски.
Пример 26. Квадратная таблица 25×25 раскрашена в 25 цветов так, что в каждой строке и в каждом столбце представлены все цвета. Докажите, что если расположение цветов симметрично относительно одной из диагоналей, то на этой диагонали тоже представлены все цвета.
Решение. Поскольку в каждой строке представлены все цвета и количество цветов совпадает с числом столбцов, то в каждой строке находится ровно по одной клетке каждого цвета. Таким образом, клеток каждого цвета – 25 штук. Далее, так как таблица симметрична относительно диагонали, то вне диагонали находится четное число клеток каждого цвета (каждой клетке соответствует симметричная). Поскольку клеток каждого цвета нечетное число, то на диагонали каждый цвет обязан присутствовать. Это и требовалось доказать.
Пример 27. В классе 30 учеников, и каждый день трое из них дежурят по классу. Может ли через некоторое время оказаться так, что каждый с каждым дежурил ровно один раз?
Решение. Рассмотрим одного из учеников. В каждом его дежурстве участвует еще два школьника. Если оказалось, что с каждым он дежурил ровно один раз, то все остальные разбились на пары. А это невозможно, так как число 29 нечетно.
Ответ. Не может.
Интернет источники:
