Мастер-класс «Загадочные круги Эйлера на уроках в начальной школе»

Айсылу ЮСУПОВА,

учитель начальных классов

Уруссинской средней общеобразовательной школы № 1

Ютазинского района

Если вы думаете, что ничего не знаете о кругах Эйлера, вы ошибаетесь. На самом деле вы наверняка не раз с ними сталкивались, просто не знали, как это называется. Где именно? Схемы в виде кругов Эйлера легли в основу многих популярных растиражированных в сети интернет изображений на определенную тему.

Давайте вместе разберемся, что же это за круги, почему они так называются и почему ими так удобно пользоваться на уроках в начальной школе.

Круги Эйлера – это графический способ, который используется, когда нужно сравнить два или более понятия, явления, способа, предмета. «КЭ» помогают выявить общее в двух или нескольких явлениях, подчеркнуть различия и обобщить знания по выбранной теме.

Пока не очень понятно, верно? Посмотрите на этот рисунок. (Фото 1)

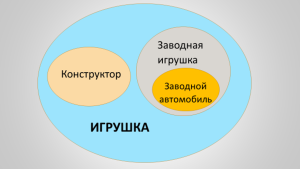
На рисунке представлено множество – все возможные игрушки. Некоторые из игрушек являются конструкторами – они выделены в отдельный овал. Это часть большого множества «игрушки» и одновременно отдельное множество (ведь конструктором может быть и «Лего», и примитивные конструкторы из кубиков для малышей). Какая-то часть большого множества «игрушки» может быть заводными игрушками. Они не конструкторы, поэтому мы рисуем для них отдельный овал. Желтый овал «заводной автомобиль» относится одновременно к множеству «игрушки» и является частью меньшего множества «заводная игрушка». Поэтому и изображается внутри обоих овалов сразу.

Ну что, так стало понятнее? Именно поэтому круги Эйлера – это тот метод, который наглядно демонстрирует: лучше один раз увидеть, чем сто раз услышать. Его заслуга в том, что наглядность упрощает рассуждения и помогает быстрее и проще получить ответ.

Автор метода — ученый Леонард Эйлер (1707-1783). Он так и говорил о названных его именем схемах: «круги подходят для того, чтобы облегчить наши размышления».

Круги делятся на группы в зависимости от типа отношений между множествами. (Фото 2)

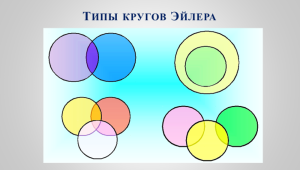
Прием «Круги Эйлера» активно применяется в рамках технологии развития критического мышления.

Как работать с приемом «КЭ»

1. На уроке выявляются два или более понятий, терминов, явлений, которые нужно сравнить.
2. Ученики рисуют кольца и заполняют графы.
3. На этапе осмысления (закрепления материала) в парах, в группах происходит обсуждение составленных диаграмм.

Этот метод можно использовать на различных уроках. Для каждого урока можно выбрать нужное количество колец — в зависимости от количества сравниваемых понятий, предметов.

Работу по обучению разделения на множества и подмножества можно начинать уже с 1 класса.

На уроках обучения письму работаем с буквами, повторяем из каких элементов они состоят, находим буквы, которые состоят из одинаковых элементов, или, наоборот, из данных элементов собираем буквы, заселяем их в домики. (Фото 3)

На уроках Русского языка с помощью кругов мы можем находить общее и различное в значении слов, сравнивать предложения разных по цели высказывания, составу, наличию или отсутствию второстепенных членов и многое другое. (Фото 4)

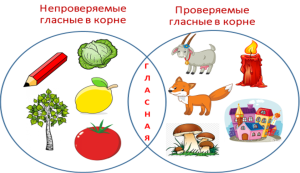
Очень хорошо применяются КЭ на уроках Окружающего мира. Дети учатся классифицировать окружающий мир по признакам, свойствам, принадлежности. Они наглядно видят, что все, что нас окружает может обладать как общими, так и отличительными признаками. (Фото 5)

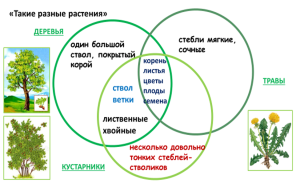
На уроках литературного чтения круги помогают работать не только над логическим мышлением, но и над развитием речи, обогащают словарный запас. Так как дети строят собственные, связные высказывания. Круги используем при работе с текстом. (Фото 6)

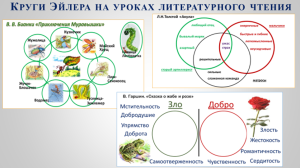
Даем сравнительную характеристику героям, сравниваем произведения. (Фото 7)

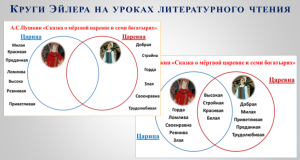
На уроках математики мы можем сравнивать фигуры, числовые выражения, даже при помощи КЭ решать задачи. Давайте, рассмотрим более подробно решение логической задачи с помощью кругов Эйлера.

Видео

Митя и Даша содержат аквариумных рыбок. Митя коллекционирует только меченосцев, а Даша – рыбок красного цвета.

У детей 8 меченосцев, а красных рыбок – 7. Всего у детей – 12 рыбок. Возможно ли такое?

Так, давайте, нарисуем аквариум Мити и аквариум Даши. В аквариум Мити мы поместим всех меченосцев, меченосцы-это такие рыбки с длинным хвостиком. А в аквариум Даши всех красных рыбок. Всех меченосцев к Мите, а Даше красных рыбок. У нас остались 3 красные рыбки. И Даша, конечно же, считает, что эти рыбки должны плавать в ее аквариуме, однако Митя не согласен, потому что эти рыбки также являются меченосцами, и он считает, что эти рыбки должны плавать в его аквариуме.

Какой выход можете предложить? Как можно было бы решить эту задачу?

Давайте, объединим аквариумы Мити и Даши. Появляется область пересечения. Эта область принадлежит как Дашиному аквариуму, так и Митиному аквариуму. Вот в этой части Дашиного аквариума только красные рыбки, в этой части Митиного аквариума только меченосцы. А на пересечение мы поместим всех наших спорных рыбок. В области пересечения расположились красные меченосцы.

В математике используют понятие множества. В Дашином аквариуме находится множество красных рыбок, а в Митином множество меченосцев. А на пересечение находятся красные меченосцы.

Если вы посчитаете рыбок, то вы увидите, что их ровно 12. Но если вы посчитаете меченосцев – 1,2,3,4,…8, то вы увидите, что их 8. А если вы посчитаете красных рыбок, то вы увидите, что их 7 – одна, две, три …7.

Итак, ситуация, которая описанная в задаче, возможна.

Данные схемы заносим в тетрадь, или работаем на рабочих листах. Обязательно учитываем дифференцированный подход. Для ребят со слабым уровнем логического мышления даем задания с готовыми кругами помощниками – названиями множеств, для ребят со средним уровнем – в задании показаны понятия, и ребята, показывающие высокий уровень – самостоятельно находят понятия и устанавливают отношения между ними.

Живые круги: А сейчас, давайте я на живом примере покажу, как действуют круги Эйлера, попробуем вместе построить круги.

Выйдите, пожалуйста, учителя, кто преподает в начальных классах….

А сейчас я прошу выйти учителей татарского языка…

И выйдите, пожалуйста, учителя, кто преподает в старших классах

Среди учителей татарского языка есть кто преподает в начальных классах? Объединитесь пожалуйста.

Вот вам наглядный пример Кругов Эйлера. Спасибо!

Забавно, правда? И главное, все сразу становится понятно. Можно потратить много слов, объясняя свою точку зрения, а можно просто нарисовать или образовать простую схему, которая сразу расставит все по местам.

Полагаю, мне удалось убедить вас, что круги Эйлера – не просто занимательная и интересная штука, но и весьма полезный метод, они помогают быстро и просто решить даже достаточно сложные и просто запутанные на первый взгляд задачи.